티스토리 뷰
코딩테스트 연습 - 정수 삼각형
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] 30
programmers.co.kr
이문제는 DP의 개념과 배열로 삼각형을 접근하는 방법만 알면 어렵지않게 풀 수 있는 문제였던것 같다.
문제풀이
-DP배열에 이전까지와 현재 값을 더한것중 큰것을 넣는다.
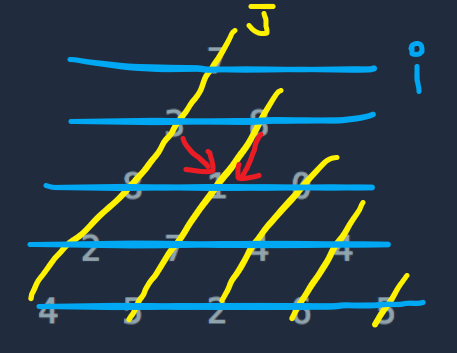
-위의 그림처럼 배열이 생성되고 따라서 빨간 화살표부분이 DP[i][j]이면 DP[i-1][j-1],DP[i-1][j]에서 내려올 수 있는 것이다.
-따라서 DP[i][j] =Math.max(dp[i-1][j-1], dp[i-1][j])+triangle[i][j] 가 된다.
-여기서 고민해 봐야할 것은 삼각형 면들에 있는 즉 j==0일때와 j==i일때의 경우에는 양쪽에서 내려오는것이 아닌 한쪽에서만 내려올 수 있다
-따라서 j==0 일때, dp[i][j] = dp[i-1][j]+triangle[i][j]
- j==1 일때,dp[i][j] = dp[i-1][j-1]+triangle[i][j] 식으로 계산 할 수 있다.
-마지막으로 삼각형의 밑변에 해당하는 마지막 배열에서 가장 큰 수가 답이 된다.
class Solution {
public int solution(int[][] triangle) {
int[][] dp = new int [triangle.length][triangle[triangle.length-1].length];
int max=0;
//꼭짓점 dp
dp[0][0]=triangle[0][0];
for(int i=1;i<triangle.length;i++){
for(int j=0;j<triangle[i].length;j++) {
//각각 경우마다 어느 경로로 온 값이 큰지 판단해서 넣어줌
if(j==0) {
dp[i][j] = dp[i-1][j]+triangle[i][j];
}
else if(j==i) {
dp[i][j] = dp[i-1][j-1]+triangle[i][j];
}else{
dp[i][j]=Math.max(dp[i-1][j-1], dp[i-1][j])+triangle[i][j];
}
//삼각형의 밑변 배열일 경우 max값을 찾아서 답으로 출력
if(i==triangle.length-1) {
max = Math.max(max, dp[i][j]);
}
}
}
return max;
}
}'CS공부 > 알고리즘&문제풀이' 카테고리의 다른 글
| [프로그래머스]2020카카오블라인드:자물쇠와열쇠(java) (0) | 2020.08.27 |
|---|---|
| [백준 15683]감시/삼성 sw역량 테스트 기출(java) (0) | 2020.08.12 |
| [프로그래머스]해시(Hash):베스트앨범(java) (0) | 2020.08.04 |
| [프로그래머스]해시:위장(java) (2) | 2020.07.29 |
| [프로그래머스]DP:N으로 표현(java) (0) | 2020.07.26 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 채팅
- java
- 정렬
- dfs
- Spring
- 자바
- 운영체제
- SWEA
- 프로그래머스
- Baekjoon
- 삼성 sw역량테스트
- sockjs
- programers
- 백준
- 최소 스패닝 트리
- BFS
- websocket
- JavaScript
- Heap
- Stomp
- OS
- DP
- 삼성 sw역량 테스트
- 알고리즘
- MST
- Oracle
- 완전탐색
- git
- 분리 집합
- 코딩테스트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
