티스토리 뷰
이 문제의 경우 그래프 탐색 유형에 속해 있으며 bfs, dfs, 플로이드와샬등 다양한 풀이 방법으로 해결이 가능하다고 한다. 처음 문제를 접했을 때는 금방 풀릴 거 같았지만 생각보다 어렵게 느꼈고 다른 분들의 풀이 방법을 참고하여 해결하였다. 플로이드 와샬이라는 방법을 몰랐기 때문에 공부하였고 이 알고리즘으로 풀이를 하였다.
-플로이드 와샬 기본문제 (백준 11404- 플로이드)
플로이드 와샬 이란?
다익스트라 알고리즘과 같이 정점-정점 간의 최단거리를 구하는 알고리즘이다.
차이점으로는
다익스트라는 하나의 고정된 정점에서 다른 모든 정점으로의 최단거리를 구하는 것이고,
플로이드 와샬은 모든 정점에서 다른 모든 정점으로의 최단거리를 구하는 것이다. 또한 dp를 기반으로 이루어진다.
문제풀이
-이 문제는 여러 가지 구슬 정렬 방법 중 어떤 경우에도 중간에 위치할 수 없는 구슬의 수를 구하는 문제이다.
-5개의 구슬 중 3개 이상 즉 전체 구슬을 n이라고 하면 (n-1)/2개 이상이 앞에 위치하거나 뒤에 위치하거나 한다면 이 구슬은 중간에 올 수 없게 되는 것.
-플로이드 와샬은 최소 경로를 찾는 것. 이를 이용해 내 앞에 위치해야 되는 구슬의 수와 뒤에 위치해야 하는 구슬의 수를 구할 수 있다.

-위의 그래프처럼 1번 구슬이 2번 구슬보다 작다면 arr [1][2] = -1 , arr [2][1] = 1
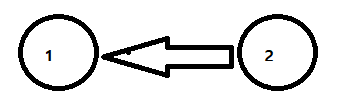
-반대의 경우는 arr[1][2] = 1, arr[2][1] = -1 이 된다.
-즉 1일 경우는 [i][j] i구슬로 들어오는 방향의 그래프 -> i보다 j가 구슬의 크기가 작아 더 앞에 위치한다는 의미.
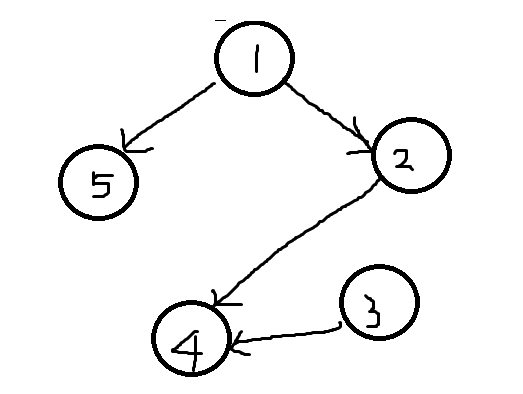
-예제의 그래프를 그려보면 이렇게 된다. 1번은 5번과 2번 앞에 있어야 하고 4번은 2번과 3번 뒤에 있어야 한다.
-자세히 보면 1번이 2번 앞에 있으려면 결국 4번 앞에 있는 2번 앞에 있어야 하므로 1번은 총 5,2,4 3개의 구슬 앞에 위치해야 된다는 조건이 생기므로 (n-1)/2개 이상에 걸려서 답이 되는 것!
-플로이드 와샬이 동작하는 방법은 예를 들어 1-4 구슬을 확인할 때 거쳐가는 구슬인 2번이 같은 방향으로 있을 경우 1-4에도 값을 체크해준다. 글보다 코드 보는 게 판단이 쉬우니 코드로 확인해보자
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Ex_2617 {
public static void main(String[] args) throws Exception{
// TODO Auto-generated method stub
// 구슬찾기 플로이드 와샬
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int[][] arr = new int[n+1][n+1];
//반의 값을 구함
int half = (n/2)+1;
while(m-- > 0) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
//크기 a>b
arr[a][b] = 1; // a가 b보다 큼 a<-b
arr[b][a] = -1; // b가 a보다 작음 b->a
}
for(int i=1;i<=n;i++) {//거쳐가는 구슬
for(int j= 1;j<=n;j++) {//출발 구슬
for(int k=1;k<=n;k++) {//도착 구슬
//구슬의 연결관계가 있을때
//출발 구슬-> 거쳐가는 구슬 , 거쳐가는 구슬-> 출발 구슬
//이런식으로 위치가 정렬되어 출발구슬이 도착구슬과 직접적인 연결이 아니어도
//위치가 지정되는 조건이 하나 더 성립됨
if(arr[k][i] != 0 && arr[j][i] == arr[i][k])
arr[j][k] = arr[j][i];
}
}
}
int[] big = new int[n+1];
int[] small = new int[n+1];
//뒤에 오는 조건, 앞에 오는 조건의 개수를 각각 세어 저장
for (int i = 1; i <= n; i++ ) {
for (int j = 1; j <= n; j++) {
if (arr[i][j] == 1)
big[i]++;
if (arr[i][j] == -1)
small[i]++;
}
}
int ans=0;
//조건이 총구슬의 반이 넘으면 답의 개수를 늘려준다
for(int i=1;i<=n;i++) {
if(big[i] >= half) ans++;
if(small[i] >= half ) ans++;
}
System.out.println(ans);
}
}
'CS공부 > 알고리즘&문제풀이' 카테고리의 다른 글
| [팰린드롬 문제] 프로그래머스,백준 풀이-Manacher's 알고리즘 (0) | 2021.02.06 |
|---|---|
| [백준 16472] 고냥이(java)-투포인터 (0) | 2021.01.28 |
| [백준 2234]bfs : 성곽(java) - 비트마스킹 (0) | 2020.12.29 |
| [프로그래머스]2018카카오블라인드:[1차] 셔틀버스(java) (0) | 2020.12.10 |
| [백준 4963]bfs : 섬의 개수(java)-메모리 초과 문제 (0) | 2020.11.29 |
- Total
- Today
- Yesterday
- programers
- 자바
- DP
- Stomp
- 백준
- 채팅
- 삼성 sw역량 테스트
- BFS
- dfs
- Oracle
- sockjs
- 삼성 sw역량테스트
- Baekjoon
- JavaScript
- MST
- 최소 스패닝 트리
- websocket
- 분리 집합
- Spring
- 완전탐색
- Heap
- java
- 코딩테스트
- OS
- git
- 프로그래머스
- SWEA
- 알고리즘
- 정렬
- 운영체제
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
